What is Gravity?

This Physics site will show a simple electric understanding of the Nature of Gravity - and that Gravity may be a pseudo-force. (Def. of pseudo = false, not authentic)

Clean up your PC and try this free spyware remover software.

	Free Fall of Elementary Particles
	"Please do not let the conservative abstract scare you off. The paper was originally written for publication in a conservative mainstream journal, but was rejected by Physical Review journal for interesting reasons. The paper contains factual scientific information on how gravity may be explained as an electromagnetic effect. The information in this paper is ground-breaking in that it may open up the door for understanding how to build artificial electro-gravity. It also opens up the possibility of voice and data communication via "gravity" waves which can be sent through solid earth and water without attenuation." -Nils Rognerud, Nov. 28, 1996


	Free Fall of Elementary Particles On moving bodies and their electromagnetic forces. ABSTRACT This paper is a review of the problem of the observable action of gravitational forces on charged particles. The author discusses the induced electric fields and the sometimes overlooked unique physical properties. He analyzes several experiments, showing the reality of the induced electric fields. The current interpretation, based on the idea of only one electric field, with certain characteristics, is compared with alternative approaches. Keywords: physics, grand unification, gravity, electromagnetic, UFO, levitation, anti-gravity. This paper can be viewed in HTML (below), or download the Free Fall of Elementary Particles paper in PDF file format.


		INTRODUCTION: Measurements of the gravitational force on elementary particles have been done for electrons (F. C. Witteborn and W. M. Fairbank ) , bulk matter (R. V. Eotvos, D. Pekar, and E. Fekete) , (G. Roll, R. Krotkov and R. H. Dicke) , neutral particles of ordinary matter (J. W. T. Dabbs, J.A. Harvey, D. Paya and H. Horstmann) and photons (R. V. Pound and J. L. Snider). No direct measurements have been done for positively charged particles. An experiment (currently on hold because of lack of funds and equipment problems) is on the way in Cern (T. Goldman, M. V. Hynes and M. M. Nieto). This experiment will attempt to measure the free fall of antiprotons. In this paper, we will show that there is a small residual electric field, due to electric dipoles, in all atomic matter. This electric field arises from the fact that two equal and opposite charges (such as a proton and it s electron cloud) generate electric effects that do not quite cancel, at distant points. Since it is expected that mother earth generates a large amount of these electric fields, it is postulated that the outcome of free falling particle experiments in Cern, and the equipment used, are dependent - to some extent - on such fields. We will show that such fields may be difficult to shield, and as such, this information may be of interest to researchers and experimental physicists.


	INDUCTION AND RELATIVITY: In the field of electromagnetism, every point in space is characterized by two vector quantities, which determine the force on any charge. First, there is the electric force, which gives a force component independent of the motion of the charge, q. We describe it by the electric field, E . Second there is an additional force component, called the magnetic force, which depends on the relative velocity, v , of the charge in relation to reference frame of the magnetic field source. - The Lorentz Force Equation says that the force on an electric charge is dependent not only on where it is, but also on how fast it is moving in relation to something else, as in:


	(2.0)


	In figure 1, a conducting rod is moving through a magnetic field B . An electron, located in the rod, sees a magnetic force due to motion of the rod through the magnetic field. In the reference frame of the magnetic source (frame S), there is no E , thus the only force acting on the electron, is:


	(2.1)


	What happens if the rod is at rest with the observer's reference frame, but the magnetic source is moving with velocity - v , as in figure 2? Does the electron stay where it is? Would we see different things happening in the two systems?


	Figure 1. A conducting rod is in relative motion with respect to a magnet. An observer S, fixed with respect to the magnet that produces the B-field, sees a rod moving to the right. He also sees a magnetic force acting downward on the electron.


	We know from relativity that magnetism and electricity are not independent things - they should always be taken together as one complete electromagnetic field. Although in the static case Maxwell's equations separate into two distinct pairs, with no apparent connection between the two fields, nevertheless, in nature itself there is a very intimate relationship between them arising from the principle of relativity. In accordance with Special Relativity, we must get the same physical result whether we analyze motion of a particle moving in a coordinate system at rest with respect to the magnetic source or at rest with respect to the particle. In the first instance the force was purely magnetic , in the second, it was purely electric . We know that a charge q is an invariant scalar quantity, independent of the frame of reference. Since the F ' equal to F , we can calculate F ' as:


	(2.2)


	For cases where the source of the magnetic field is moving, the relative velocity v becomes the opposite sign. To distinguish this type of motional electric field, we can rewrite the equation, where V is the relative velocity, and B is the magnetic field (seen by S):




	since we know that


	(2.3)

		(2.4)


	Figure 2. A conducting rod is in relative motion with respect to a magnet. An observer S' fixed with respect to the rod, sees the magnet moving to the left. He also sees an electric force acting downward on the electron.


	Mathematically, it can be shown that a purely electric field in one reference frame can be magnetic in another. The separation of these interactions depends on which reference frame is chosen for description. In 1903 - in a now famous experiment - Trouton and Noble showed that two electric charges moving with same constant velocity do not produce a magnetic interaction between themselves. This is consistent with the fundamental postulate of relativity. The force between two electric charges must be the same for an observer at rest with respect to the charges. This is true whether the charges move at constant velocity, or whether they remain fixed with respect with some reference frame. Since electric and magnetic fields appear in different mixtures if we change our frame of reference, we must be careful about how we look at the fields E and B. We must not attach too much reality to them. The field lines may disappear if we try to observe them from different coordinate systems. The field lines that we see in our textbooks for electric and magnetic fields are only mathematical constructs to help us understand and clarify the effects more easily. We can say more accurately that there is such a thing as a transformed electromagnetic field with a new magnitude and direction. Einstein's special relativity and Lorentz transformation make this view possible.


	THE MOTIONAL ELECTRIC FIELD: We can further illustrate the effect of the motional electric field. When a conducting rod sees a magnetic field from a moving magnet (see figure 3), each electron in the rod experiences a force due to its relative motion through the field. If the direction of the motion of the magnet is such that a component of the force on the electrons is parallel to the conductor, the free electrons will move along the conductor. The electrons will move until they are balanced by equal and opposite electrostatic forces. This is because electrons collected at one end of the conductor, will leave a deficit of electrons at the other.


	Figure 3. The moving source of a magnetic field produces an induced motional electric field Em, which is balanced by the electrostatic field, Es. The electric field is seen by an observer stationary with respect to the rod. An electrostatic shield around the rod does not influence the experiment.


	While the motion continues, an observer inside the rod sees a zero electric field because of


	(3.0)


	where Es is the electrostatic field. A remarkable observation is that this experiment can be done with or without electrostatic shielding around the conductor. It is worth noting that the Em field is quite different from the Es field in that the boundary condition for Em is equal to the boundary conditions for the magnetic field. (More on this later.) In the equilibrium state, the observer in the reference frame of the moving rod will not feel any forces due to electric fields, either Es or Em. This conclusion has some profound effects on our experiments. For example, one cannot connect a voltmeter to the moving rod (that is stationary with respect to the rod) and expect to see a motional electric potential, Em. All wires of the voltmeter and the voltmeter itself will be equally polarized, in a manner similar to the rod. Understanding this concept is important, as it may be one of the fundamental reasons why the motional electric field often goes undetected.


	MAGNETIC INFLUENCES IN A ZERO B-FIELD: In the general theory of quantum electrodynamics, one takes the vector and scalar potentials as the fundamental quantities in a set of equations that replace the Maxwell equations. E and B are slowly disappearing from the modern expression of physical law; they are being replaced by the vector potential, A and scalar potential, O. Feynman says the vector potential is not just a mathematical convenience, but is introduced because it does have an important physical significance (Feynman) . Lets review a few of examples: - The Long Solenoid - The Electron Interference Experiment - Two Moving Magnet Experiment - The Hooper Coil The Long Solenoid: It is easy to agree that a long solenoid carrying an electric current has a B-field inside - but none outside. If we arrange a situation where the electrons are to be found only outside of the solenoid, we know that there will still be an influence on the motion of electrons - as this is the workings of the common electrical transformer. This phenomena has always been of interest to students, because the induction in the wires takes place in a region of space where the resultant magnetic flux is reduced to zero. How could this be? According to classical physics this is impossible, as the force depends only on B, yet we use this transformer principle in common electronic components. It turns out, that quantum mechanically we can find out that there is a magnetic field inside the solenoid by going around it - even without ever going close to it. We must use the vector potential, A , as shown in figure 4. Alternatively, if we are not too concerned about the zero B-field in the region of the electron, we can also use Faraday's Law of Induction. This law states that the induced electromotive force is equal to the rate at which the magnetic flux through a circuit is changing, as in


		(4.0)

	Figure 4. The magnetic field and the vector potential of a long solenoid.


	In the case of the long solenoid, it turns out that both the classical and quantum calculations give the same result.


	The Electron Interference Experiment: Physical effects on charged particles - in a zero B-field - have been studied since the 1950s. The reader is advised to refer to quantum interference of electrons (S. Olariu and I. Iovitzu Popescu) , for further study. Although this is a very important subject, we encourage the reader to investigate this area for himself. Bohm and Aharanow show in their electron interference experiment that a magnetic field can influence the motion of electrons even though the field exists only in regions where there is an arbitrarily small probability of finding the electrons. Two Moving Magnets Experiment: Magnetic flux is constructed from two sources, as in figure 5. Both magnets move uniformly in opposite directions with a speed V producing an Em on the electron, inside the conductor. We can find the total Em field by superposition, as follows:


	(4.1)


	Since B and V are equal in magnitude for both magnets, we find by vector addition the total induced electrical field, as follows:


	(4.2)


	We notice that the induced electrical field is twice that from a single magnet, while the sum of B is remarkably - zero. This experiment is easy to setup and verify in any electronics laboratory with a pair of magnets, a wire and a voltmeter. In fact, you may wrap the conductor, in an electrostatic or magnetic shielding, and find the same result.


	Figure 5. An electron, in a conductor, experiences a force due to the flux from two moving magnetic sources.


	The Hooper Coil: The author has tested a setup by pulsing strong currents, opposite and equal, through multiple parallel conductors. The configuration of the conductors in this type of experiment will cancel the B-fields, while still producing an Em field, in accordance with Eq. 4.2. This is similar to an experiment by Hooper (W. J. Hooper) , who successfully predicted and measured the motional electric field - all in zero resultant B-field. Interestingly, all of the above experiments can influence an electron with a zero B-field, in the region of the electron. This has some profound implications - one of which is that the motional electric force field is immune to electrostatic or magnetic shielding. Experimentally, it can be confirmed that the motional electric field is immune to shielding and follows the boundary conditions of the magnetic (not electric) field. The only way to shield a motional electric field is to use a magnetic shield around the source of the magnetic flux - containing it at the source. These effects are not startling if one remembers that the motional electric field is a magnetic effect and that a magnetic field has a different boundary condition than the electric field.


	DIELECTRIC EFFECTS FROM DIVERGENT ELECTRIC FIELDS: Most textbooks in physics describe how a piece of paper or a neutral dielectric object can be picked up with a charged glass rod. This is the divergent electrical field at work. It polarizes and generates a net attraction on the dielectric object. A dielectric object is always drawn away from a region of a weak field towards a region of a strong field, as seen in figure 6. The polarity of the field does not affect the direction of the force.


	Figure 6. A non-uniform electrical field will generate a net attractive force on a neutral piece of matter. The force is directed toward the region of higher field strength. The net force on the dielectric is proportional to the gradient of the square of the field times the volume of the dielectric (P. Lorrain and D. Corson) , given by :


	(5.0)


	where Vedv is the effective dielectric volume, is the permittivity constant and is the dielectric constant for hydrogen. We do not know the effective dielectric volume for a single hydrogen atom, but we can estimate it by using the classical size for the Bohr atom and adjust the radius with a factor kedv:


	(5.1)


	We can calculate the divergent Em field from a hydrogen atom due to the motion of the electron charge. Knowing the magnitude and divergence of the Em field, we can find the force that pulls on a nearby atom, in accordance with Eq. (5.0). In view of quantum mechanics, the Bohr model is an over-simplification. However, as we will see, this approach offers some insights into the nature and magnitude of the force generated by the divergent motional electric field. It is very much like Feynman's calculation of the atomic magnetic moment using classical mechanics (Feynman) that turns out to be quite accurate


	Figure 7. An orbital electron with a linear velocity v is producing a motional electric field Em at P.


	The magnetic field from an orbital electron is found by using the Biot-Savart law:


	(5.2)


	r is the radius vector from q to a point P where B is measured, and v e is the electron velocity. Since the electron revolves at a radial frequency




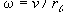	the B-field "velocity", V at a distance r can be calculated as


	The motional electric field E m is then found by inserting Eq. (5.2) into Eq. (2.3):


	(5.3)


	By expanding and simplifying Eq. (5.3) we get a large symbolic expression. Figure 5 shows a plot of the E m vector fields around the hydrogen nucleus according to such a formula. The plot shows that the x-components of the vectors are always in the same direction, regardless of the electron position about the nucleus. It can also be seen that all y-components are opposite, in the upper and lower quadrants. Assuming a full uniform circular orbit of the electron, the y-components will cancel while the x-components will add. For a full revolution, the hydrogen atom will generate a net E m field in the negative x-axis direction - measured at point P.


	Figure 8. The 2-dimensional vector plot of the motional electric field - produced by the orbital electron around the hydrogen nucleus. All measurements are done at a stationary point P, with x=1 meter and y=0 from the nucleus.


	It is worth noting that the electron spin itself does also generate a motional electric field. This effect will be ignored in our discussion since it can be shown that it falls off faster than the motional electric field produced by the circulating electron. It may be speculated that the motional electric fields generated by spinning elementary particles has some relationship to nuclear forces, but this is not discussed here. Since a hydrogen atom can be considered a tiny dielectric, it is attracted towards the source of a diverging E m field. We can calculate the instantaneous force generated by the diverging E m field from Eq. (5.0). The instantaneous force for various positions of the moving electron is plotted in figure 9. Assuming that the y-components will cancel we can find the sum of the x-components. When measured at point P, the sum of all the x-vectors will not completely cancel, due to a small difference in magnitude between distance R+x and R-x. Mathematically, the dielectric force produced by a single atom acting on another dielectric atom can be found by integrating one revolution of the moving electron (ignoring the y and z components, for now) by using Eq. (5.0):


	(5.4)


	where and alpha is the angle of the electron to the x-axis and r0 is the electron radius.


	Figure 9. A 2-dimensional vector plot of the instantaneous dielectric force, produced by an electron moving around the nucleus of a hydrogen atom. All measurements are done at point P with x=1 meter and y=0.


	The expanded equation is large and is not easy to simplify symbolically. However, the equation can be calculated numerically by computer. We will use the following constants:


	We arbitrarily adjust the volume for a single hydrogen atom from Eq. (5.1) by setting kvol=1/1000 . By using Eq. (5.4), we then can find the dielectric force between two hydrogen atoms to be:


	(5.5)


	GRAVITATIONAL FORCES ON ELEMENTARY PARTICLES: Lets compare the force calculated in Eq. (5.5) - due to the diverging Em field - with Newton's Law for a force between two hydrogen atoms. The gravity force between two hydrogen atoms can be calculated as follows:


	(6.0)


	Note the similarity in magnitude between Eq. (6.1) and Eq. (5.5). The equations have the same power with distance. Is gravity simply a pseudo-force caused by the relativistic effects of moving charges - calculated as the divergent Em field? Perhaps gravitation may due to the fact that we do not have the right coordinate system? Curiously, the divergent atomic Em field does have all the characteristics of gravity, such as a non-shieldable force that follows the inverse square of distance law. Atoms that generate an Em field will give rise to nearby electrostatic fields that are set up to counter balance anything that is polarized by such Em fields. If we ignore the effects of particle spin, it means that there are no net forces on a single charged elementary particle suspended in a gravitational field - that is, if it is located inside a closed box of normal matter. We can predict that a single positive or negative elementary particle will "float" in a gravitational field, as if with no weight. However, a dielectric (such as a neutral atom) will fall in the same situation. It may be argued that elementary particles have no weight at all - and that they only have only inertia and mass. Interpretation of results from a free fall experiment of electrons at Stanford University (F. C. Witteborn and W. M. Fairbank ) may suggest that elementary single particles do not have weight. The results from Stanford University showed that the gravitational acceleration of electrons in a metal tube was close to zero (measured to within 9%). The scientists explained this unusual result as the effect of the earth gravitational pull on free electrons in metal. It was argued that each electron and nucleus in the metal were acted on by an average electrical field (set up by a slight displacement of charges), polarizing the metal and exactly counteracting the free floating electrons inside the tube. According to the divergent Em field theory, the experiments at Stanford, could be explained by understanding that there are no forces on non-dielectric charged particles (such as an electron) located in cavity immersed in an Em field. The electrostatic field, setup inside the cavity to counteract to the Em field, will exactly cancel the Em field because of separation of charges. Understanding this, a single electron will behave as having no weight, since Em - Es = 0, and the electron will appear to have no acceleration in a gravitational field. Complete atoms and molecules - with dielectric constants greater than zero - will accelerate in a divergent Em field. As discussed earlier, the Em fields generated by ordinary matter cannot be measured directly by electronic means. This is because the Em fields can not be shielded and all instrumentation and wires are polarized so there are no currents. This effect will may cause us to think that there is no Em field present. However, we will see the dielectric force that is similar in magnitude to the force of gravity. In free space, protons, located away from other objects, will accelerate if they are in a divergent Em field. This is due to the electrical Em field that will act directly on the elementary charges without any counteracting electrostatic fields. Interestingly, the Earth's atmosphere does measure an electrostatic potential voltage gradient of approximate 100 V/m. Is this the electrostatic field that the ionosphere produces to counteract an Em field generated by mother Earth? The Earth's electrostatic field does have the correct polarity to support such a theory. No theory so far seems to explain why the Earth electrostatic field is never depleted despite all the lightning and discharging of energy. The Em field theory explains this puzzling effect as the continuos polarization of the ionosphere, generated by the atomic matter of Earth. Due to this effect, the ionosphere will never be discharged.

		Summary: We have seen how it possible for two hydrogen atoms to generate a non-shieldable force of similar magnitude to gravity. This effect is due to the motional electric field produced by each atom. The dielectric hydrogen atoms will attract towards each other because of the divergent electric fields, produced by each atom. The dielectric force equation in Eq. (5.5) between two hydrogen atoms has a similar magnitude to that of gravity and follows the same inverse square law of force. Further, the divergent Em field theory postulates that elementary particles will have mass and inertia, but no weight. It is predicted that a charged particle, like the antiproton, will not accelerate in a gravitational field when it is located in a cavity of neutral matter - up or down. The antiproton will only accelerate in the opposite direction of the divergent electrical Em field (as produced by the Earth) if the antiproton has a dielectric constant greater than zero. It is assumed that elementary particles, such as the antiproton, has a dielectric constant much smaller than that of atoms or molecules, and therefor will not accelerate appreciably in the divergent Em field when compared to the acceleration of a neutral atom. The free fall experiment in CERN will be a crucial test for the true nature of anti-protons and the gravitational field. It is postulated that gravity is simply the dielectric pseudo-force due to the relativistic motions of orbital electrons of ordinary matter. I challenge you to apply the knowledge and help build a better world.

		ACKNOWLEDGMENT: The late Dr. William J. Hooper is acknowledged for his valuable inspiration about the unique physical properties of the motional electric field.

		REFERENCES: - F. C. Witteborn and W. M. Fairbank (1967). Phys Rev. Lett., 19, 1049 - R. V. Eotvos, D. Pekar, and E. Fekete, Ann. Physik 68, 11 (1922) - G. Roll, R. Krotkov and R. H. Dicke, Ann Phys. (N.Y.) 26, 442 - J. W. T. Dabbs, J.A. Harvey, D. Paya and H. Horstmann, Phys. Rev. 139, B756 (1965) - R. V. Pound and J. L. Snider, Phys. Rev. 140, B788 (1965) - T. Goldman, M. V. Hynes and M. M. Nieto, Gen Rel. and Grav.18, 67 (1986) - Feynman, "The Feynman Lectures on Physics", 6th printing, (Addison Wesley, Massachusetts, 1977), vol II, p. 15-8 - S. Olariu and I. Iovitzu Popescu, "The quantum effects of electromagnetic fluxes", Rev. Mod. Phys., 57, 339-435. - W. J. Hooper, U.S. Patent No. 3.610.971, 1971 - P. Lorrain and D. Corson, "Electromagnetic Fields and Waves", 2nd ed. (W. H. - - Freeman, New York, 1970), p. 126 - Feynman, "The Feynman Lectures on Physics", 6th printing, (Addison Wesley, Massachusetts, 1977), vol II, p. 34-3 - F. C. Witteborn and W. M. Fairbank (1967). Phys Rev. Lett., 19, 1049